“New Corner” competition

About the “New Corner” competition

The “New Corner” competition is designed to help student’s explorer their talents and passion for informatics and computational thinking with engaging competitions. Participation in these competitions has a very small registration fee (350MKD) and the tasks can all be completed without any preparation or studying. Students from 6 to 21 years old work through a set of tasks that focus on different topics and skills within informatics and computational thinking. They will have 50 minutes to complete as many tasks as they can, they are not expected to finish them all. The competition has seven different age categories with each their own set of tasks to keep things exciting and challenging for all students:

Category 1 (age 6-7)

Category 2 (age 8-10)

Category 3 (age 10-12)

Category 4 (age 12-14)

Category 5 (age 14-16)

Category 6 (age 16-18)

Category 7 (age 18-21)

Each group will get 3 sets of 4 tasks. The 3 sets each have a level of difficulty: easy, medium or hard.

Examples

Though there is no need to prepare for the contest,
you might want to get a feel for the style of the tasks.
There are sample questions shown below to do so:

Example 1

Commands

Very easy applications have only a few commands. A command tells something (or someone) what has to be done. Which of these lines could be seen as an easy application

Answers:

A) What is data?

B) Come in and close the door!

C) One plus one is two

D) Welcome home!

Solution:

B) Command-1 is "come in", Command-2 is "close the door". It works properly, if you start being outside, and the door is open, and you execute the commands sequentially. What happens to you executing the program with the door being closed?

Answer A) is not a program but a question. C) is an equation, but nothing to do. D) is a message for somebody, but it is nothing to do.

It's Informatics: Commands and data are fundamental principles of informatics. Commands tell the computer what it should do with data, or computers can instruct actuators (things that do something in the real world) to perform an action in the real world. Many commands can be expressed as a program for humans, for robots, for computerised gadgets, etc. To express something, language is needed. It is not yet decided whether the natural human languages, spoken or written, in the long term will be easily useable for programming. People working in Informatics research this problem. So far, logical, and very strictly structured calculuses serve as programming "languages". If you learn to program, you have to learn how to properly transform natural language-based ideas about the what to do into syntactically correct and semantically almost error-free command sequences.

Example 2

Glasses

There are five drinking glasses on the table. One of them is turned upside down.

A line drawing of a cup Description automatically generated with medium confidence

In this game, you have to get all glasses upright again. But: you have to turn exactly three glasses every turn. How many turns do you need at least to get all the glasses standing upright?

Answers:

A) 2 turns

B) 5 turns

C) 3 turns

D) it is impossible!

Solution: C

For example:

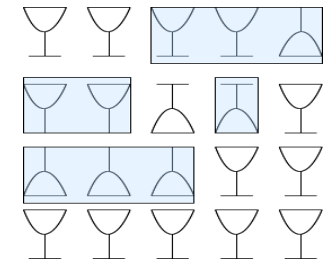
Notice that there must be an odd number of turns, since after the first turn, there will be either 2 or 4 glasses which are upside-down. On the next turn, there will be an odd number (1,3,5) of glasses which are upside-down. Thus, we require more than 2 moves and in general we require an odd number of moves. We have shown a solution which uses 3 turns, which must be the minimum. It's Informatics: Following an algorithm, we can keep track of the state of the system or its variables. Reasoning about parity and arguing correctness for an algorithm are important aspects of informatics. One possible way to analyse the solution is to consider either deterministic finite automata (self-operating machines) or to consider a breadth-first search.

Recognition and Reward: Winning or performing well in computational thinking competitions can provide participants with recognition and rewards, such as prizes, scholarships, or opportunities for further education or career advancement. These incentives can motivate individuals to push themselves further and strive for excellence in their computational skills.

Take part in the biggest online competition in Computational thinking and win valuable prizes!

· I prize: 500 Euros

· II prize: 300 Euros

· III prize: 100 Euros

2025-09-15

https://sochistroygroup.ru/ - строительные советы онлайн

2025-09-15

Для работы на смартфоне используйте http://krakr.cc/, мобильная версия доступна без перебоев.

2025-09-18

Вкупно 0 MKD

Вашата кошничка

Вкупно 0 MKD

Вашата кошничка

Вкупно 0 MKD

Вашата кошничка

Вкупно 0 MKD

“New Corner” competition

Deadline April 09, 2025

GregoryLoove

JasonPsymn

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

krakrRic

krakrRic

krakrRic

krakrRic

krakrRic

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

CesarVes

krakrRic

krakrRic

krakrRic

krakrRic

krakrRic

krakrRic

krakrRic